技術者ならこれだけは知っとけ！

技術系に関して、備忘録になるようまとめて記載していきます。解説項目については極力誰にでもわかるように解説していきたいと思います。

技術系力学公式集（流体力学）

工学系公式集

よく使う単位

名称 記号 単位 備考
粘性係数 \mu Pa ・ s Pのポアズと表示することもある
動粘性係数 \nu = \frac {\mu} {\rho } m^{2} / s Stのストークスと表示することもある
レイノルズ数 Re = \frac {UD} {\nu} - D：代表長さ、U：速度、 \nu ：動粘性係数
ヌセルト数 N = \frac { \alpha L } { \lambda } - L：代表長さ、 \alpha ：流体の熱伝達率、 \lambda ：流体の熱伝導率　
フルード数 F = \frac { U } { \sqrt { g h } } - １より大きければ斜流となり、小さいと常流となる。　斜流から常流に移行する際に　跳水現象が発生する。（慣性力/重力）　
ウェーバー数 W= \frac { \sigma } { \rho U ^ { 2 } L } - （表面張力/慣性力）
温度拡散率 \alpha = \frac { \kappa } { \rho C _ { p } } - \kappa :熱伝導率
プラントル数 P _ {r} = \frac { \nu } { \alpha } = \frac { \frac { \eta } { \rho } } { \frac { \kappa } { \rho C _ { p } } } = \frac { \eta C _ { p } } { \kappa } -　 air:0.7程度、water:0.7以上、liquid metal:0.7未満になる。 (動粘性係数/温度拡散率）
グラスホフ数 G _ { r } = \frac { g \beta Δ L ^ { 3 } } { \nu ^ { 2 } } - (浮力/粘性率）　 G_{r} ＞1 の場合自然対流が支配的。　
レイリー数 　 R _ { a } = G _ { r } ・P _ { r } - 臨界レイリー数 1708（上下面が固定）、1108（下面が固定）を越えると自然対流により乱流へ移行する　

表面張力による剪断応力

\tau = \frac { F } { A } = \mu ・ \frac { U } { h }

力F=粘性係数μ×速度U×面積A÷水膜の厚さh

W=F・U [W=J/s]

層流と乱流

層流

Reが2300以下

乱流

Reが4000以上

層流と乱流の混合域

2300 ＜ Re ＜ 4000

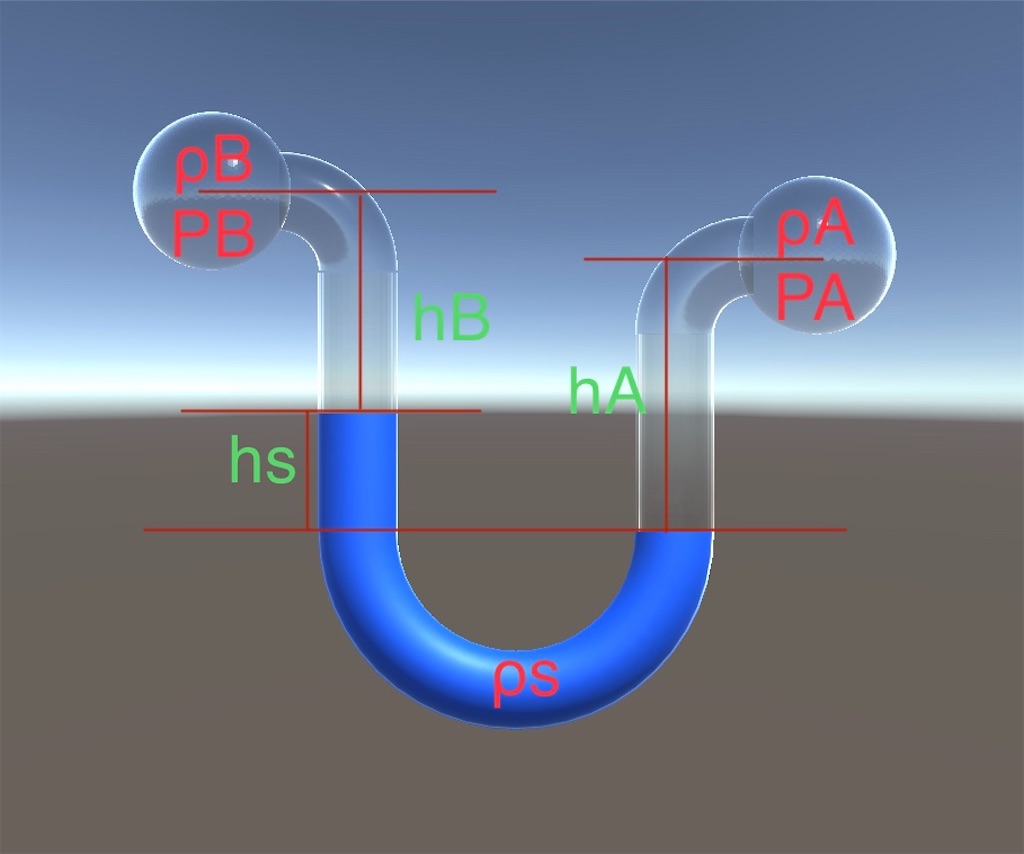
マノメーター

P _ { A } + \rho _ { A } g h _ { A } = P _ { B } + \rho _ { B } g h _ { B } + \rho _ { s } g h _ { s }

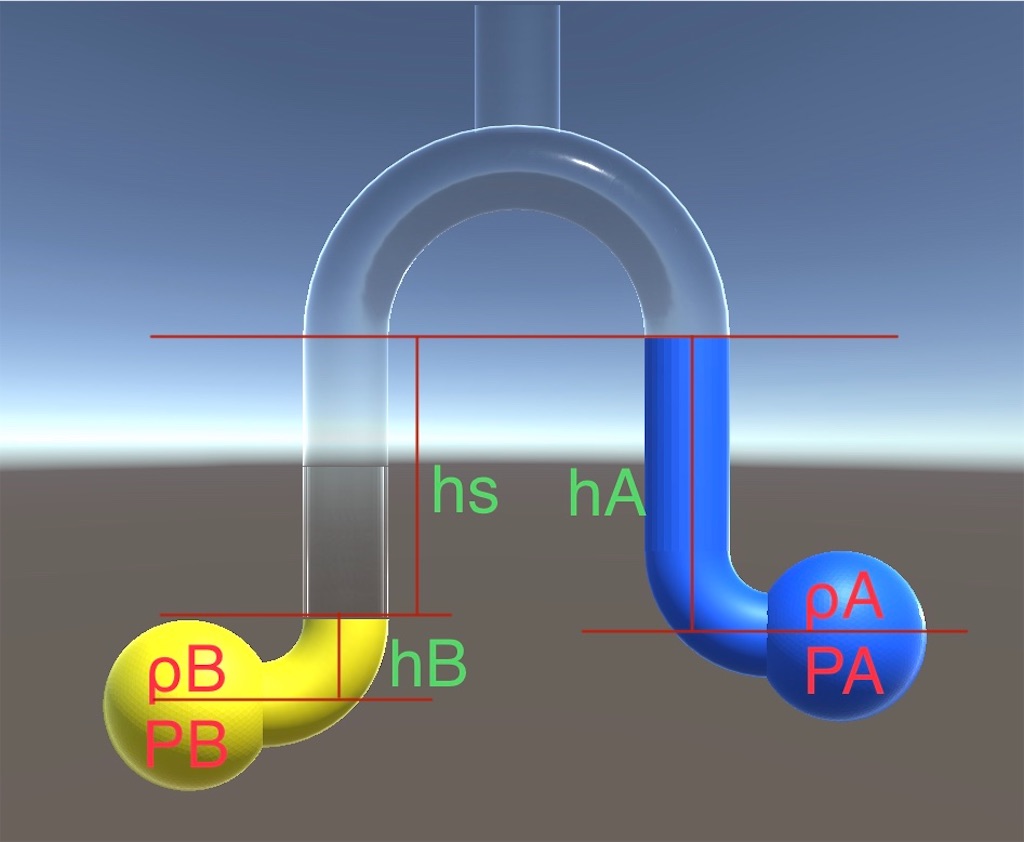
反転マノメーター

P _ { A } + \rho _ { A } g h _ { A } = P _ { B } + \rho _ { B } g h _ { B } + \rho _ { s } g h _ { s }

浮力

f:id:mmt726zushi:20191222205747j:plain

F= \rho g h _ { 2 } A - \rho g h _ { 1 } A = \rho g ( h _ { 2 } - h _ { 1 } ) A

( h _ { 2 } - h _ { 1 } ) A = V より

F= \rho g V

連続の式

f:id:mmt726zushi:20191227233355p:plain

Q = A U = const

\rho Q = \rho A U = const

ベルヌーイの定理

f:id:mmt726zushi:20191227235114p:plain

P _ { 1 } + \frac { 1 } { 2 } \rho v _{1} ^ { 2 } + \rho g h _ { 1 } = const

トリチェリの定理

f:id:mmt726zushi:20191222180945j:plain

P + \frac { 1 } { 2 } \rho v _ { 1 } ^ { 2 } + \rho g h= P + \frac { 1 } { 2 } \rho v _ { 2 } ^ { 2 }

v _ { 1 } = 0 より

\rho g h = \frac { 1 } { 2 } \rho v _ { 2 } ^ { 2 }

\therefore v _ { 2 } = \sqrt { 2 g h }

容器からの流出時間

T = \sqrt　{ \frac { 2 h } { g } } \frac { A } { A _ { 0 } }

mmt726zushi-engineer.hatenablog.jp

流体の運動量

F = \rho Q u = \rho A u ^ { 2 }

９０°曲げ配管（水平方向右から鉛直方向下に向き変更）

f:id:mmt726zushi:20191222165630j:plain

PA + \rho Q u = T とすると

\therefore F = \sqrt { 2 } T

mmt726zushi-engineer.hatenablog.jp

\theta 曲げ配管　（水平方向右から時計回りに \theta 向き変更　）

f:id:mmt726zushi:20191222205744j:plain

PA + \rho Q V =T とすると

\therefore ( PA + \rho Q u ) \sqrt { { 2 } ( 1 - cos \theta ) }

ダルシーワイズバッハの式

Δ h = \lambda \frac { L } { D } \frac { U ^ { 2 } } { 2 g }

管摩擦係数

層流時（ R e = ＜ 2 3 0 0 ）の管摩擦係数はReに反比例する。

\lambda = \frac { 6 4 } { R e }

ムーディ線図を用いることで、相対粗さ、Re、管摩擦係数より導き出すことができる。

圧力損失

損失ヘッド

損失した圧力を位置エネルギーに換算する考え方。

Δ h = \frac { Δ P } { \rho g } を損失ヘッドと呼ぶ

mmt726zushi-engineer.hatenablog.jp

圧力損失から流量を導く

Δ P = Δ h ・ \rho g = \lambda \frac { L } { D } \frac { U ^ { 2 } } { 2 g } ・ \rho g

\lambda = \frac { 6 4 } { R e }

より

Δ P = \frac { 6 4 } { R e } \frac { L } { D } \frac { U ^ { 2 } } { 2 g } ・ \rho g

R e = \frac { U D } { \nu } = \frac { U D \rho } { \mu }

より

Δ P = \frac { 64 \mu } { U D \rho } \frac { L } { D } \frac { U ^ { 2 } } { 2 g } ・ \rho g

流量Qは流速Uと配管の断面積の積に等しいため

Q = U ・ 1/4 \pi D^ { 2 }

U = \frac { Q } { 1/4 \pi D ^ { 2 } }

となり、Uを代入すると

Δ P = \frac { 64 \mu } { U D \rho } \frac { L } { D } \frac { U } { 2 g } ・ \rho g \frac { Q } { 1 / 4 \pi D ^ { 2 } }

Δ P = \frac { 128 \mu L Q } { \pi D ^ { 4 } }

\therefore Q = \frac { \pi D ^ { 4 } Δ P } { 128 \mu L }

配管の出入り口の圧力損失

損失ヘッドの式、また、動圧は \frac { 1 } { 2 } \rho U ^ { 2 } = ΔP と表現できるため

Δ h = \frac { Δ P } { \rho g } = \frac { U ^ { 2 } } { 2 g } 　となり

これに係数をつけると

Δ h = \zeta \frac { U ^ { 2 } } { 2 g } となり

\zeta の部分が変化する。

1.配管出口→タンク

\zeta = 1

f:id:mmt726zushi:20191221141105p:plain

2.タンク→配管入口

\zeta ＜ 0.5 は配管入り口のR形状に依存し。Rがない場合最大となる。

f:id:mmt726zushi:20191221141107p:plain

ブラジウスの式（管摩擦係数）

\lambda = 0.3164 Re ^ { - 0 . 2 5 }

3000＜　Re ＜80000

揚力と抗力

f:id:mmt726zushi:20191227190629p:plain

物体が画像左方向に進んでいるとすると。

\frac { 1 } { 2 } \rho V ^ { 2 } S C _ { L }

\frac { 1 } { 2 } \rho V ^ { 2 } S C _ { D }

カルマン渦

Re ＜ 6 の時

渦の発生はなく、物体の表面に沿って流れる

6 ＜Re ＜ 40 　の時

双子渦という後方に２つの渦が同時に発生する

40 ＜ Re 　の時

物体の後方上下に交互に渦が発生する

これをカルマン渦という。

ストローハル数

S _ { t } = \frac { f d } { U }

Re = 5 \times 1 0 ^ { 2 } 〜 2 \times 1 0 ^ { 5 } 　の時

S _ { t } = 0 . 2 となる。

境界層

流速の99%を境界層という

層流時の流れ（ハーゲン・ポアユイズ流れ）

Rが配管径、中心からの距離r離れた場所での流速をuとする。

f:id:mmt726zushi:20191228141656p:plain

\alpha を圧力勾配とする。

u= \frac { \alpha } { 4 \mu } ( R ^ { 2 } - r ^ { 2 } )

Q = \frac { \pi \alpha } { 8 \mu } R ^ { 4 }

毛細管現象

\rho g \pi r ^ { 2 } h = 2 \pi r T cos \theta

h = \frac { 2 T cos \theta } { \rho g r }

境界層厚さ

\sqrt { \frac { \nu x} {U}}

剪断応力

\mu U \sqrt { \frac{ U } { \nu x } }