圧力損失(損失ヘッド)
流体によって曲げ配管にかかる力
工業力学【剛体(円柱)の滑り運動(並進運動)&ころがり運動(回転運動)】

1.問題
剛体の滑り運動&ころがり運動の問題
角度αの斜面に置いた半径R[m]、質量m[kg]の円柱が
①斜面をころがらずに滑った場合と
②滑らずに転がった場合の
[t]秒後に移動した距離x[m]を求めよ。
初期速度は0[m/s]とする。

①斜面をころがらずに滑った場合
まず運動方程式を立てます。
高校物理でやる【質量×加速度=合力】です。
質量:m
加速度:
合力:F
なので
(1)となります。
重力による力mgは斜面方向成分のみを考えるため
(2)となります。
(1)の式に(2)式を代入すると
(3)となります。
式(3)の両辺をmで割ると
(4)となります。
この式より斜面を滑る物体は質量に依存しないことがわかります。
(4)式の両辺をdtで積分すると
(5)となります。
は速度
です。 (
)
初期条件t=0の時v=0であるため
となり、
(6)となります。
(6)の両辺を再度dtで積分すると
となり、
初期条件t=0の時x=0であるため
となり、
(7)となります。
(7)の式より、t秒後にどれだけ滑ったか(x)が求められます。
②滑らずにころがった場合
同様に運動方程式を立てますが今回はころがり運動をするため、摩擦力Fが進行方向と逆方向にかかります。
上の図の様にころがった角度をθと置くと運動方程式は以下になります。
(8)
【質量×加速度=合力】
(9)
回転にかかる運動方程式は
【慣性モーメント×角加速度=合力×回転中心からの距離(トルク)】となります。
慣性モーメントって何?って思うかと思いますが、慣性モーメントは別の機会にご説明します。
「質量が物体の動かし難さ」と考えれば慣性モーメントは「物体の回転し難さ」です。
質量が大きければ大きいほど動かすのに力が必要ですが、
慣性モーメントも同様に大きければ大きいほど回転させるのに力(合力×回転中心からの距離:トルク)が必要になります。
円柱が円周方向に回転する場合の慣性モーメントは
となります。
回転量θと進んだ距離xとの関係を考えてみる。
まず円周を求める式はご存じですよね?
そう、2πrですよね。
円柱を1周転がしたとき進む距離は何になるでしょうか?
そう、2πrです!
πとは180°という意味ですので、この式の2πとは360°ということだったんですね。
つまり何が言いたいかというと、
ころがった角度に半径をかけてあげると、転がった距離が導けるのです!
つまり (10)となります。
(11)に変形できます。
のθに(11)の式を代入すると(問題文では半径がRなためr=Rを代入)
(12)となるため
(9)式に(12)を代入すると
(13)となる。
(13)式に を代入すると
となり、きれいに半径Rが消え、
(14)となります。
この式より転がり運動は半径に依存しないことがわかります。
(14)式のFを(8)式に代入すると
変形すると、
(15)となりmが両辺からなくなり、
この式より質量にも依存しないことがわかります。
(15)式の両辺をdtで積分すると
初期条件t=0の時v=0であるため
(16)となる。
(16)式の両辺を再度dtで積分すると
となり、
初期条件t=0の時x=0であるため
(17)となる。
(17)の式より、t秒後にどれだけ転がったか(x)が求められます。
2.滑り運動(並進運動)&ころがり運動(回転運動)の式を比べてみる。
(7)
(17)
ころがり運動は滑り運動に比べて同じ時間に進む距離が()になることがわかります。
3.目で確認
最後に一番上に物理演算させた動画を載せていますので、物体がどう動くのか目で確認してください。
工業力学のまとめは以下をご覧ください。
材料力学(引張荷重による棒の伸び)
1.問題
引張荷重による棒の伸びの問題
下図赤矢印の方向にPの力が働いた時の矢印の方向の伸びを求めよ。
引張荷重:P
断面積:A
材料の長さ:L
ヤング率:E
とする。
unityで記載

jwwで記載

2.公式の確認
応力:σ
引張ひずみ:ε
伸び:λ
とすると以下となる。
3.公式の導出
式(2)のεに式(3)を代入すると、
式(1)のσに式(4)を代入すると
これをλ=の式に整理すると
となる。
材料力学のまとめは以下をご覧ください。
技術系力学公式集(熱力学)
- よく使う単位
- 仕事
- 熱量
- 熱力学第0法則
- 熱力学第1法則
- 熱力学第2法則
- エンタルピとは
- エネルギー保存
- ボイルの法則
- シャルルの法則
- ボイルシャルルの法則
- 気体の状態変化
- ポリトロープ指数
- 1モルの標準状態
- ダルトンの法則
- 気体の状態方程式
- 気体定数
- サイクル
- エクセルギー
- 空燃比
- 燃空比
- 理論空気量
- 空気過剰率
- 当量比
- 理論的空燃比
- 発熱
- 熱伝導
- 対流伝熱
- 熱抵抗
- 温度境界層
- 輻射伝熱
- 黒体、黒体面
- 放射エネルギー
- ステファンボルツマンの法則
- 灰色体、灰色面
- 物体の温度が一定ということは・・・(キルヒホッフの法則)
- 熱交換器
よく使う単位
| 名称 | 記号 | 単位 | 備考 |
|---|---|---|---|
| 熱量 | ジュール | |
1cal=4.2J |
| 力 | ニュートン | |
[1kgを |
| 圧力 | パスカル | |
|
| 動力 | W | |
|
| 熱容量 | |
|
|
| 比熱 | |
|
|
| 熱流束 | |
|
|
| 熱伝導率 | |
|
|
| 温度伝導率 | |
|
熱伝導率を密度と定圧比熱で割ったもので大きいほど熱が伝わりやすい |
| 熱伝達率 | |
|
|
| 熱通過率 | |
|
|
| エントロピ | |
|
|
| エンタルピ | |
|
H=U + PV |
| 電気使用率 | |
|
*1 |
仕事
仕事=力×距離
1Nは1kgの物体を に加速させる力。
仕事÷時間=仕事率、動力
熱量
熱量=質量×比熱×温度変化量
c:比熱
1gの純水を1℃高める熱量
4.1868J =1cal
圧力一定
定圧比熱:
体積一定
定容比熱:
マイヤーの式
比熱比
標準状態の水の体積
原子結合による比熱比の差
| 結合原子数 | 比熱比 |
|---|---|
| 単原子 | |
| 2原子 | |
| 多原子 | |
熱力学第0法則
熱は高いところから低いところに行くだけ。
熱力学第1法則
エネルギー保存
dQ=dU+PdV
dQ=dH-VdP
熱力学第2法則
熱を100%仕事に変換することはできない。
エンタルピとは
内部エネルギーと圧力の持つエネルギーであるため、エネルギーは保存される。
H=U+PV [J]
h=u+pv [J/kg]
テスト等では[kJ/kg]の問題が多いので注意
エネルギー保存
気体が持つ全体のエネルギーは保存されるため
エンタルピー+運動エネルギー+位置エネルギー=constとなる。
全体のエネルギーをEとし、熱量Qを加えた時に仕事Lを取り出せたとすると。
初期状態を1とすると
となる
すなわち仕事は加えた熱量から内部エネルギーの変化量を引いた分となる。
ここから、運動エネルギー及び位置エネルギーの変化がないとするとE=Hとなるため
は基本的にマイナスの値をとる。
となる
ボイルの法則
PV=const
シャルルの法則
T=273.15+温度[℃]
ボイルシャルルの法則
気体の状態変化
| 変化名称 | ポリトロープ指数 | 状態計算 | 仕事及び内部エネルギー |
|---|---|---|---|
| 等圧変化 | |
|
|
| 等温変化 | |
|
|
| 等容変化 | |
|
|
| 断熱変化 | |
|
|
ポリトロープ指数
以下式に該当する状態変化のポリトロープ指数を代入することで、気体の状態を計算することができる。
| 変化名称 | ポリトロープ指数 |
|---|---|
| 等圧変化 | |
| 等温変化 | |
| 等容変化 | |
| 断熱変化 | |
1モルの標準状態
(1気圧、0℃)=22.4L
ダルトンの法則
理想気体を混合した時、混合後の圧力(全圧)は、混合前に存在した時の圧力(分圧)の和に等しくなる。
気体の状態方程式
m[kg]
n[mol]
気体定数
サイクル
| サイクル名 | サイクル | 効率 | 備考 |
|---|---|---|---|
| カルノーサイクル | ①等温膨張 ②断熱膨張 ③等温圧縮 ④断熱圧縮 | |
|
| オットーサイクル | ①断熱圧縮 ②等容加熱 ③断熱膨張 ④等容放熱 |
|
圧縮比が大きいほど、比熱比が大きいほど効率UP |
| ディーゼルサイクル | ①断熱圧縮 ②等圧加熱 ③断熱膨張 ④等容放熱 |
|
を締切比と呼ぶ。 |
| ランキンサイクル | ①断熱圧縮 ②等圧加熱 ③断熱膨張 ④等圧放熱 |
エクセルギー
全エネルギー内の理論上取り出せる仕事量のことで、高温部の熱量とカルノーサイクルをかけたものを言う。
しかしエクセルギー全てを利用することはできないため、どれだけエクセルギーを使用できたか表す指標を有効エクセルギーという。
有効エクセルギー効率は(実際に得られる仕事÷エクセルギー)で求められる。
空燃比
空気質量を燃料質量で割った無次元量
燃空比
燃料質量を空気質量で割った無次元量
理論空気量
燃料を完全燃焼されるために必要な空気量
空気過剰率
使用空気量/理論空気量=空気比(空気過剰量)
当量比
空気過剰量の逆数
理論的空燃比
使用空気量と理論空気量が同じの状態を理論的空燃比と呼ぶ
発熱
低発熱量=高発熱量ー水蒸気の凝縮潜熱と水の蒸気の量
熱伝導
mmt726zushi-engineer.hatenablog.jp
対流伝熱
温度の異なる流れを生じた流体により、固体の熱量が移動する現象。
熱抵抗
物体の熱伝導、熱伝達率、厚さなどを考慮し、熱の移動を抵抗として捉える考え方。
電気の抵抗と同様に熱抵抗は以下の式により求められる。
熱伝導により伝わる熱量の式は以下となるため
熱伝達により伝わる熱量の式は以下となるため
熱抵抗の合成
この合成抵抗が大きいほど断熱性が高いと判断できる。
温度境界層
対流電熱の際に流体 の温度が固体
の温度まで変化している層のこと
輻射伝熱
物体からの放射(波)により熱が伝わることをいう。 対流がないにもかかわらず熱の移動が発生する物を言う。
ハロゲンヒーターをイメージするとわかりやすいかと。
黒体、黒体面
全体波長のエネルギーを反射せず吸収できる理想物体であり、最も多く放射エネルギーも放出する。
放射エネルギー
プランクの法則より黒体が絶対温度Tであった時の波長λのエネルギーを以下の式で示すことができる。
ステファンボルツマンの法則
放射エネルギーを求めるプランクの法則は定められた波長λのみのエネルギーとなるため
全エネルギーを求める場合に用いる
放射エネルギーは温度の4乗に比例する。
この をステファンボルツマン定数という。
灰色体、灰色面
下の式に示す理論上の黒体との放射エネルギーの割合を放射率と言い、このような物体を灰色体と呼ぶ。
物体の温度が一定ということは・・・(キルヒホッフの法則)
吸収する熱量と、放射する熱量が同じということ。
これをキルヒホッフの法則という
熱交換器
高温流体と低温流体の熱を交換する熱交換器の移動する熱量は以下の式で求められる。
並流式と向流式があり を求める式が異なる。
並流式
高温流体と低温流体が同じ方向に流れる間に熱交換を行う方式
高温入口温度ー低温入口温度
高温出口温度ー低温出口温度
向流式
高温流体と低温流体が逆方向に流れる間に熱交換を行う方式
高温入口温度ー低温出口温度
高温出口温度ー低温入口温度
平流式よりも が大きく熱交換による熱の移動量が大きくなる。
*1:例:10[Wh]とは10Wを1時間使用した場合の電力量。すなわち10[Wh]=10[W]×3600[s]=36000[J]=36[kJ]に等しい
技術系力学公式集(工業力学)
随時更新
慣性モーメント
1.円柱の中心軸周り
2.円板の直径軸周り
3.球
4.正方形の中心軸周り
5.角柱(回転軸に対して垂直な面の辺の長さをw、lとする)
6.細長い棒の先端周り
平行軸の定理
hは重心を通る回転軸に平行な距離
剛体の回転運動

より
↓詳細は以下
mmt726zushi-engineer.hatenablog.jp
運動方程式
剛体の運動方程式
剛体の角運動方程式
運動エネルギー保存
運動量保存
運動量保存
角運動量保存
とする時
を代入すると
すなわち
振動
1.引張ばね
固有角振動数
固有振動数
周期
2.ねじりばね
固有角振動数
固有振動数
3.振り子ばね
が
になる
固有角振動数
固有振動数
減衰振動
cを減衰係数と呼ぶ
運動方程式は以下となる。
1.  の時
の時
過減衰となり振動せずに減衰する
2.  の時
の時
臨界減衰と呼ばれる状態となる。
時間とともに収束するがcが少しでも小さくなると不足減衰になる。
3.  の時
の時
不足減衰となり振動しながら減衰する、減衰振動となる。
臨界減衰係数
減衰比
減衰が働いた時の固有角振動数
は必ず正となるため
となり、
減衰すると固有角振動数は小さくなる。
周期が大きくなる、すなわちゆっくりになる。
また を展開すると
となる。
技術系力学公式集(材料力学)
- 応力
- 引張荷重による伸び
- ヤング率
- 歪み
- 自重による伸び
- 応力拡大係数
- 断面2次モーメント
- 梁のたわみ
- 片持ち梁
- 両端支持梁
- 軸のねじり
- 軸にかかるトルクと伝達動力
- 熱応力
- 座屈
- 歪みエネルギー
- 薄肉円筒にかかる応力
随時更新公式集です。
応力
引張荷重による伸び
↓詳細は以下
mmt726zushi-engineer.hatenablog.jp
ヤング率
歪み
自重による伸び
応力拡大係数
断面2次モーメント
| 形状 | 断面二次モーメント I | 断面係数 Z |
|---|---|---|
円形  |
|
|
円筒  |
|
|
正方形  |
|
|
長方形  |
|
|
長方形の断面2次モーメント導出
であるため
これを解く
長方形の断面係数導出
eは中立軸からの端までの距離であるため
より
となる
梁のたわみ
たわみ角
たわみ量
片持ち梁
より
でたわみ角が0となるため
すなわち
両端支持梁
なため
でたわみ量
のため
でたわみ角
のため
軸のねじり

比ねじり角
変形量は同じなため
材料の伸びフックの法則と同様に
ある半径 の点においての剪断応力
を代入し計算
(範囲は0からRになる)
軸にかかるトルクと伝達動力
軸のねじりの式を用いる
仕事W=力F 距離(回転させた量
)であるため
であるため
となる
回転数は基本的にrpm(rotations per minute)で記載するため、
回転数をN [rpm]とすると仕事率W[J/s = W]は
となる
1分間に行う仕事A[J=N・m]は以下となる
熱応力
座屈
断面2次半径
細長比
オイラーの公式
※Cの値は柱の支持方法により異なる。
(1)固定端と自由端:1/4
(2)回転端と回転端:1
(3)回転端と固定端:2
(4)固定端と固定端:4
図の横軸はCの値を示している。
目視でわかる様に記載してみた。

歪みエネルギー
外力により物体が変形した時の変形により物体内部に蓄えられるエネルギーのことを言う。
歪エネルギーは変形させた仕事に等しくなる。
バネ
バネをL伸ばす歪エネルギーを求める。
バネをx伸ばした時の力Fはフックの法則より
となる。
そして仕事Wは力Fと変形量xの積となるため、力Fで微小変形量dx分変形させたとすると
これを0からLで積分すると
これを積分すると以下になる
そして仕事Wと歪エネルギーは等しいため
となる。
引っ張り垂直応力による歪エネルギー
これを より整理すると以下になる。
カスティリアーノの定理
全歪エネルギーから付加された荷重で偏微分するとその荷重点におけるたわみが求められる。
0からLまでに付加された歪エネルギーを求める式は以下
片持ち梁の場合 より
これをカスティリアーノの定理より荷重Pで偏微分すると以下になる
薄肉円筒にかかる応力
軸方向にかかる応力
円周方向にかかる応力(フープ応力)
これは軸方向の2倍の応力がかかると覚えておくと早い。
技術系力学公式集(流体力学)
- よく使う単位
- 表面張力による剪断応力
- 層流と乱流
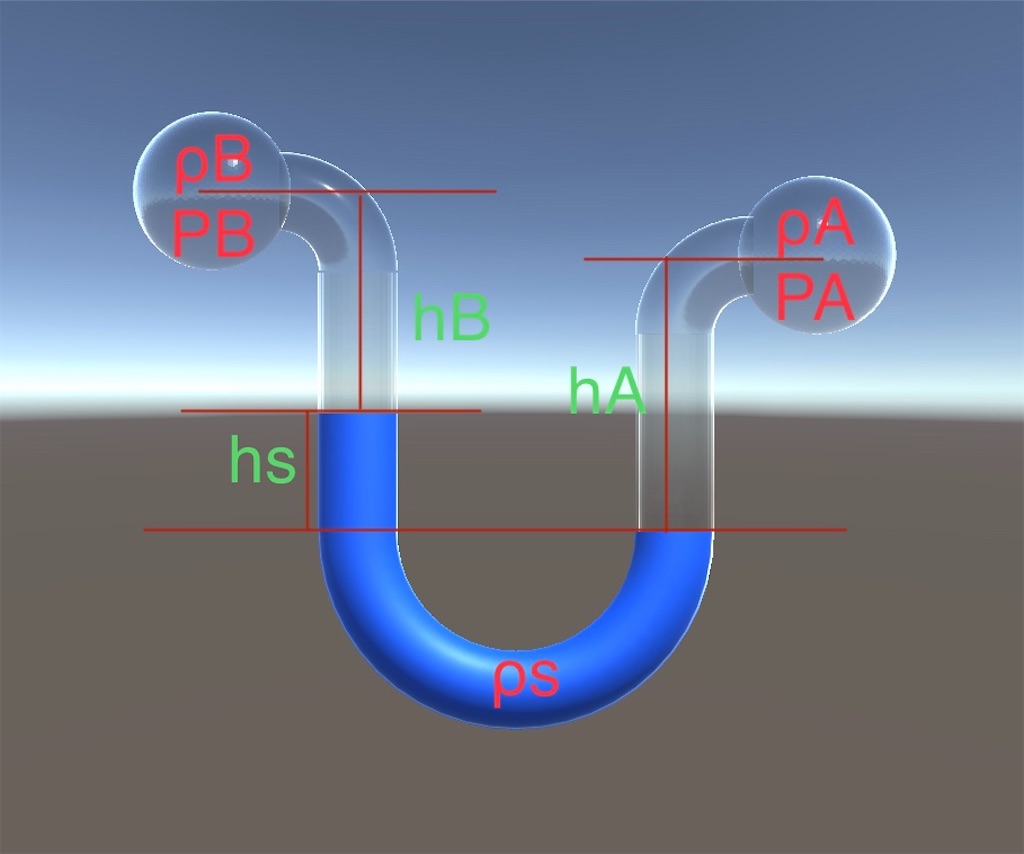
- マノメーター
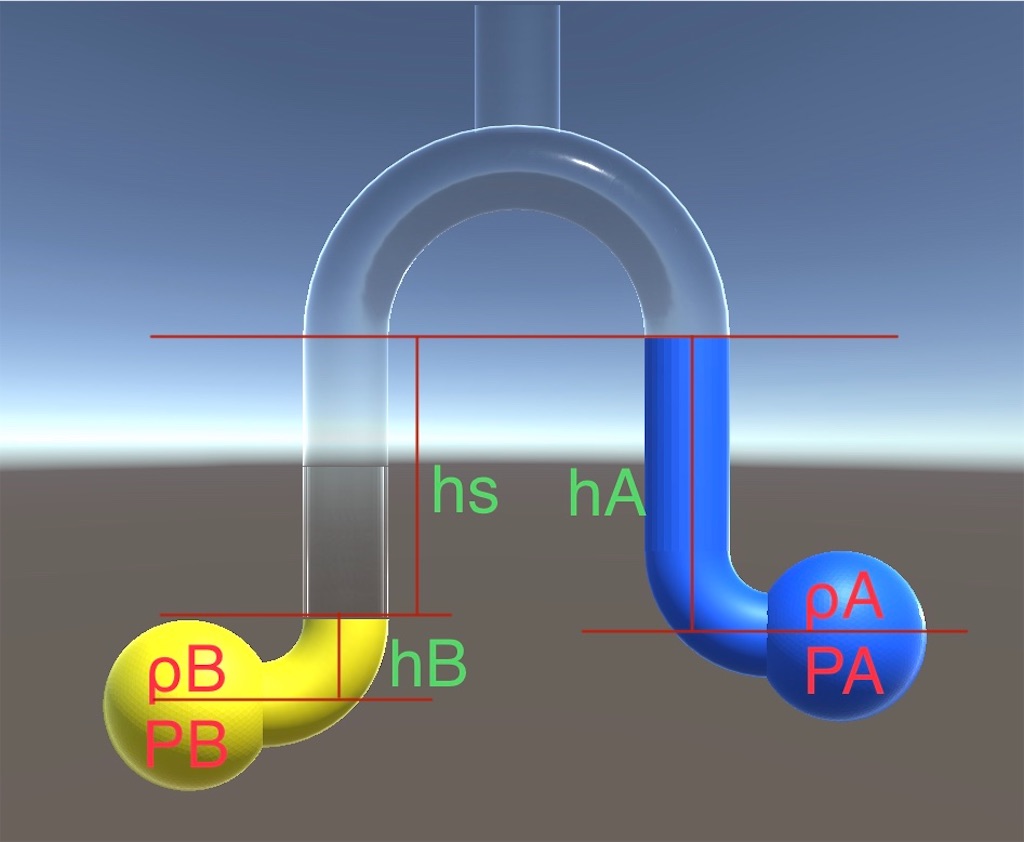
- 反転マノメーター
- 浮力
- 連続の式
- ベルヌーイの定理
- トリチェリの定理
- 容器からの流出時間
- 流体の運動量
- ダルシーワイズバッハの式
- 管摩擦係数
- 圧力損失
- 揚力と抗力
- カルマン渦
- 境界層
- 層流時の流れ(ハーゲン・ポアユイズ流れ)
- 毛細管現象
- 境界層厚さ
- 剪断応力
よく使う単位
| 名称 | 記号 | 単位 | 備考 |
|---|---|---|---|
| 粘性係数 | |
|
Pのポアズと表示することもある |
| 動粘性係数 | |
|
Stのストークスと表示することもある |
| レイノルズ数 | |
- | D:代表長さ、U:速度、 |
| ヌセルト数 | |
- | L:代表長さ、 |
| フルード数 | |
- | 1より大きければ斜流となり、小さいと常流となる。 斜流から常流に移行する際に 跳水現象が発生する。(慣性力/重力) |
| ウェーバー数 | |
- | (表面張力/慣性力) |
| 温度拡散率 | |
- | |
| プラントル数 | |
- | air:0.7程度、water:0.7以上、liquid metal:0.7未満になる。 (動粘性係数/温度拡散率) |
| グラスホフ数 | |
- | (浮力/粘性率) |
| レイリー数 | |
- | 臨界レイリー数 1708(上下面が固定)、1108(下面が固定)を越えると自然対流により乱流へ移行する |
表面張力による剪断応力
力F=粘性係数μ×速度U×面積A÷水膜の厚さh
[W=J/s]
層流と乱流
層流
Reが2300以下
乱流
Reが4000以上
層流と乱流の混合域
マノメーター
反転マノメーター
浮力

より
連続の式

ベルヌーイの定理

トリチェリの定理

より
容器からの流出時間
mmt726zushi-engineer.hatenablog.jp
流体の運動量
90°曲げ配管(水平方向右から鉛直方向下に向き変更)

とすると
mmt726zushi-engineer.hatenablog.jp
 曲げ配管 (水平方向右から時計回りに
曲げ配管 (水平方向右から時計回りに  向き変更 )
向き変更 )

とすると
ダルシーワイズバッハの式
管摩擦係数
層流時( )の管摩擦係数はReに反比例する。
ムーディ線図を用いることで、相対粗さ、Re、管摩擦係数より導き出すことができる。
圧力損失
損失ヘッド
損失した圧力を位置エネルギーに換算する考え方。
を損失ヘッドと呼ぶ
mmt726zushi-engineer.hatenablog.jp
圧力損失から流量を導く
より
より
流量Qは流速Uと配管の断面積の積に等しいため
となり、Uを代入すると
配管の出入り口の圧力損失
損失ヘッドの式、また、動圧は と表現できるため
となり
これに係数をつけると
となり
の部分が変化する。
1.配管出口→タンク

2.タンク→配管入口
は配管入り口のR形状に依存し。Rがない場合最大となる。

ブラジウスの式(管摩擦係数)
揚力と抗力

物体が画像左方向に進んでいるとすると。
カルマン渦
の時
渦の発生はなく、物体の表面に沿って流れる
の時
双子渦という後方に2つの渦が同時に発生する
の時
物体の後方上下に交互に渦が発生する
これをカルマン渦という。
ストローハル数
の時
となる。
境界層
流速の99%を境界層という
層流時の流れ(ハーゲン・ポアユイズ流れ)
Rが配管径、中心からの距離r離れた場所での流速をuとする。

を圧力勾配とする。